Cat… amarphisms

Posted on April 15, 2018

One of the first higher-order functions most students encounter in a functional programming course is the fold (foldr, foldl). A fold takes an operator, an initial value and a list, and then recursively combines each element in the list using the initial value and the given operator.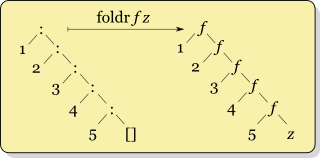
The recursive combining structure of a fold

The Easy Stuff

A catamorphism is a generalization of the fold on lists
Kmett, E. (2014, 15 Apr) Catamorphisms. School of Haskell
. The word catamorphism has its roots in the Greek word ‘κατά’ meaning ‘downwards’
(HaskellWiki, Catamorphisms)[https://wiki.haskell.org/Catamorphisms]
. In this case it is the concept of applying a fold on any algebraic data type. An algebraic data type is any data type composed of other types – as an example, take the following data type for a binary tree I will use throughout this post.
data Tree a = Empty
  | Leaf a
  | Node (Tree a) (Tree a)

The following two functions both take such a Tree and recursively combines it into an Int. The first function calculates the depth, and the second how many leaves are in the tree.
depth :: Tree a -> Int
depth Empty = 0
depth (Leaf a) = 1
depth (Node l r) = 1 + max (depth l) (depth r)

count :: Tree a -> Int
count Empty = 0
count (Leaf a) = 1
count (Node l r) = (+) (count l) (count r)

I think you can quickly see where I am going with this. These two functions both have the same structure, where for each constructor there is a function which takes some values and outputs something, sometimes recursively. Note the types of the functions used on the right-hand side of both depth and count.

The type signature of the function used when handling an Empty is just an Int. For a Leaf a we implicitly get some type a, which is then thrown away, and give an Int so its type is (a -> Int). The (+) in the case of the count function for a Node takes 2 parameters, both Ints. So, when trying to generalise count and depth we need some group of functions (Int, a -> Int, Int -> Int -> Int) for the different cases. We can now define the generic function we will use to create depth and count.
foldTreeToInt :: (Int, a -> Int, Int -> Int -> Int) -> Tree a -> Int
foldTreeToInt (empty, leaf, node) = fTreeToInt
  where
    fTreeToInt Empty = empty
    fTreeToInt (Leaf a) = leaf a
    fTreeToInt (Node l r) = node (fTreeToInt l) (fTreeToInt r)

-- We can now easily define depth and count by specifying
-- the group of functions
depth' :: Tree a -> Int
depth' = foldTreeToInt (0, const 1, \l r -> 1 + max l r)

count' :: Tree a -> Int
count' = foldTreeToInt (0, const 1, (+))

The group of functions needed for the fold is called an F-algebra and maintains the structure of the underlying algebraic data type
Jeuring, J., Swierstra, D. (2011) Languages And Compilers. Utrecht University
. We can generalise the fold we created to generic data types.
type TreeAlgebra a t = (t, a -> t, t -> t -> t)

foldTree :: TreeAlgebra a t -> Tree a -> t
foldTree (empty, leaf, node) = fTree
  where
    fTree Empty = empty
    fTree (Leaf a) = leaf a
    fTree (Node l r) = node (fTree l) (fTree r)

When the constructors are used as the functions in the algebra, we get as output the same tree. This specific algebra is called the initial algebra and defines the identity function. The count and depth functions created using the algebra and fold are called compositional functions.

Black magic

Catamorphism is a term from category theory, of which my knowledge is anything but formal (or correct). Best to hear it from someone who knows what they are talking about
Jones, C (2014, 30 Jan) Catamorphisms in 15 Minutes!
.

A F-algebra contains an endofunctor f, an object a and a morphism f a -> a
Milewski, B. (2014) Category Theory for Programmers
. A functor is a mapping between categories, where an endofunctor maps a category into itself. This can be written in haskell as type Algebra f a = f a -> a
Milewski, B. (2013, 1 Oct) Understanding F-Algebras. School of Haskell
.

We can use fixed points as our initial algebra. A fixed point here is when you can apply some functor f to itself and get the same type, possible in haskell as newtype Fix f = Fix { unFix :: f (Fix f) }. The code for writing generic catamorphisms can now be written as.
type Algebra f a = f a -> a
newtype Fix f = Fix { unFix :: f (Fix f) }

cata :: Functor f => Algebra f a -> Fix f -> a
cata f = f . fmap (cata f) . unFix

We can use cata to define count and depth after setting up the Functor instance of our Tree and the initial algebra. We also have to remove the explicit recursion from our Tree definition.
data Tree' a b = Empty'
  | Leaf' a
  | Node' b b

instance Functor (Tree' a) where
  fmap f Empty' = Empty'
  fmap f (Leaf' a) = Leaf' a
  fmap f (Node' l r) = Node' (f l) (f r)

type FTree' a = Fix (Tree' a)

count'' :: FTree' a -> Int
count'' = cata phi
  where
    phi Empty' = 0
    phi (Leaf' a) = 1
    phi (Node' l r) = l + r

depth'' :: FTree' a -> Int
depth'' = cata phi
  where
    phi Empty' = 0
    phi (Leaf' a) = 1
    phi (Node' l r) = 1 + max l r

The functions count'' and depth'' on the following example tree would evaluate to 3 and 4 respectively.
--  /\
-- 3 /\
--  1  \
--      2
example :: FTree' Int
example = node (leaf 3) (node (leaf 1) (node empty (leaf 2)))
  where
    empty = Fix Empty'
    leaf x = Fix (Leaf' x)
    node l r = Fix (Node' l r)